CSAW CTF 2021 (Qualifiers) - Forgery

"Forgery" is a crypto challenge in CSAW CTF 2021 Qualifiers. You can download the challenge file here.

Details

To solve the challenge, we would need to forge a signature that says "Cisco", "Felicity" or "both". Upon closer inspection, the signature scheme is the ElGamal signature scheme. The main giveaway is how signatures are verified:

pow(g, m, p) == (pow(y, r, p) * pow(r, s, p)) % p

gm =? yr rs mod p

Notice that the message m is verified, not its hash digest! This is key because it essentially allow the attacker to forge valid signatures on random messages. Why? That's because we could "choose" a r and s value and reverse them to find the corresponding message m. We could do the following:

1. randomly select e from 2 to p-1
2. compute r = gey mod p

Now, gm = yr (gey)s = yrgesys mod p. If ys = y-r mod p, then gm = ges mod p. We do not need information on the secret key x to compute both r and s!

So, to forge the signature, one would compute s = -r mod (p-1), which causes ys = y-r mod p. We have to mod (p-1) instead of p because s and r are used as integers rather than as group elements. Finally, compute the message of the signature, m = es mod (p-1).

def eforge(p, g, y):
    while True:
        e = randint(2, p-1) # select random v
        r = (pow(g, e, p) * pow(y, 1, p)) % (p) # r = g^e . y mod p
        s = (-r) % (p-1) # s = -r mod p-1
        m = e*s % (p-1)
        return m, r, s

But wait! we can't control m! How are we suppose to include "Cisco", "Felicity" or "both" in it? Now that we can forge existential signatures (m, r, s), we could also forge arbitrary signatures using Bleichenbacher's attack if and only if the verifier accepts a r > p. Unfortunately, that's not the case for this challenge due to the following check:

if any([x <= 0 or x >= p-1 for x in [m,r,s]]):
    return False

However, there is one subtle problem about how the challenge "accepts" our answers. The first check it does it by running this conditional:

if b'Felicity' not in answer_bytes and b'Cisco' not in answer_bytes and b'both' not in answer_bytes:

Notice, it doesn't check if answer_bytes is EXACTLY the strings that we should forge. It merely checks if the strings are part of the answer_bytes. This opens a possibility of simply adding our answer to the random signature, in hopes that the verifier "verifies" the signature part while disregarding the strings that we append/prepend. One peculiar line in the verification function confirms this possibility:

MASK = 2**1024 - 1
m = int(answer, 16) & MASK

Nice! This means that the lower 1024 bits of the answer is preserved, while any bits above 1024 bits, or 128-bytes are disregarded during verification. To solve the challenge, we would simply do the following:

m0, r0, s0 = eforge(p, g, y)
# append our target
forged = m0.to_bytes((m0.bit_length() + 7) // 8, 'big')
forged = b'both\x00\x00\x00\x00' + forged
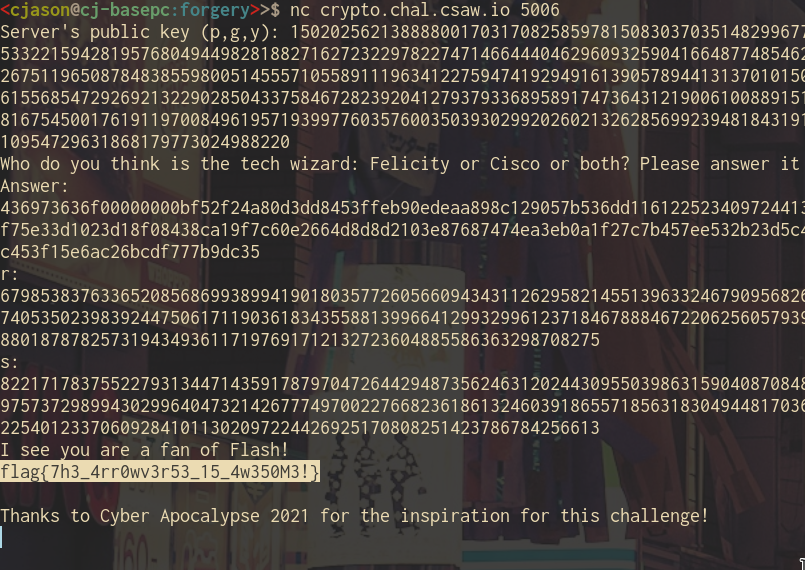
ah = forged.hex()

Then, we send ah, r0 and s0 through the netcat connection and get the flag.

Hashing the message before signing is important!